|
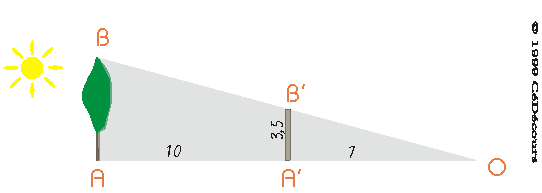
L'ombre
de l'arbre s'étend jusqu'au point O .
Le poteau est placé de
sorte que son sommet coïncide avec la limite supérieure de
la zone d'ombre. Les dimensions sont indiquéees en mètres
(m). |
| Question 1: Les
côtés du triangle OA'B' sont proportionnels : |
|
aux
côtés du triangle ABA' |
|
aux
côtés du triangle OAB |
|
aux
côtés du triangle AB'A' |
|
| Question
2: Les rapports suivants sont-ils égaux ? |
|
OA'/OA
et A'B'/AB |
|
A'A/B'B
et OA'/OA |
|
A'B'/AB
et OB'/OA' |
|
| Question
3: Grâce au théorème de Thalès on peut calculer
: |
|
la
distance du soleil connaissant la hauteur du poteau |
|
le
nombre de feuilles dans l'arbre |
|
la
hauteur de l'arbre connaissant la hauteur du poteau |
|
| Question
4: La hauteur de l'arbre est donnée par la proportion : |
|
7/17
= 3,5/AB |
|
17/7=3,5/AB |
|
7/17=AB/3,5 |
|
| Question
5: La hauteur de l'arbre est donnée par quelle relation ? |
|
AB
= (3,5 . 7) / 17 |
|
AB
= (3,5 . 17) / 7 |
|
AB
= (17 . 7) / 3,5 |
|
| Question
6: La hauteur de l'arbre est : |
|
5,8
m |
|
18,5
m |
|
8,5
m |
|
| Question
7:La longueur OB est égale à : |
|
17
m |
|
19
m |
|
21
m |
|
| Question
8 : Au cours d'une tempête, l'arbre a été en partie
déraciné. Son tronc n'est plus vertical. Pourquoi les relations
précédentes ne sont plus valables ? |
|
L'arbre
a perdu des branches |
|
L'arbre
n'est plus assez solide |
|
Le
poteau et l'arbre ne sont plus parallèles |
|
| Question
9 : L'arbre, après cette tempête, s'est incliné précisément
de 20° vers le poteau. La fin de la zone d'ombre s'est-elle déplacée
? |
|
à
gauche de O |
|
à
droite de O |
|
reste
en O |
|
| Question
10 : Est-ce que si l'on penchait aussi le poteau avec la même inclinaison,
on pourrait à nouveau appliquer le théorème de Thalès
pour trouver la hauteur de l'arbre ? |
|
oui |
|
non |
|
peut-être |
|
|
|
Copyright ©
1999 CéDécoursTM
Tous droits de propriété
intellectuelle et industrielle réservés
Il n'est en aucun cas permis de
télécharger ou d'enregistrer les images et animations présentées
ci-dessus