Lorsque l'un des côtés du triangle est un diamètre de son cercle circonscrit, alors, l'angle opposé à ce côté est droit et le triangle est rectangle.

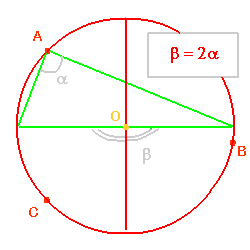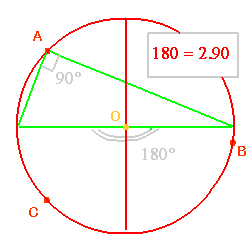
Les médiatrices des 3 côtés du triangle sont concourantes au centre du cercle circonscrit du triangle : cette propriété te permettra de retrouver le centre du cercle circonscrit.

Pour tracer le cercle circonscrit, c'est à dire le cercle qui passe par les quatre sommets du quadrilatère, il faut trouver un point (s'il existe ...) qui soit équidistant des 4 sommets.
Une méthode consiste à construire les médiatrices de chaque côté : tous les points d'une médiatrice d'un côté sont équidistants des 2 sommets qui limitent ce côté. Ensuite, si les médiatrices des 4 côtés sont sécantes, et, si elles sont concourantes en un même point, alors ce point est le centre du cercle circonscrit.

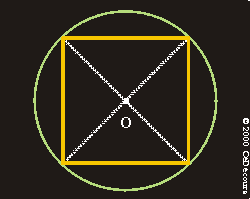
Pour le carré et le rectangle, les médiatrices sont concourantes au point 0 qui est le point de rencontre des diagonales :
O est le centre du cercle circonscrit.

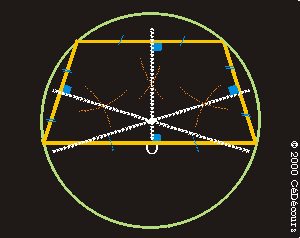
Pour le trapèze isocèle, la construction soigneuse au compas des médiatrices permet de placer le point O qui est le point de concours des médiatrices.

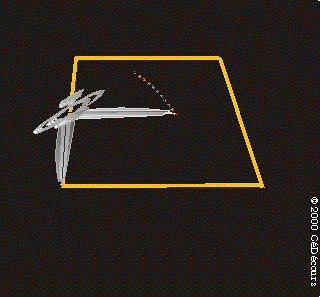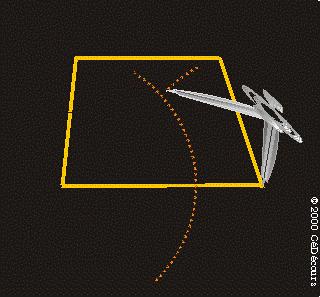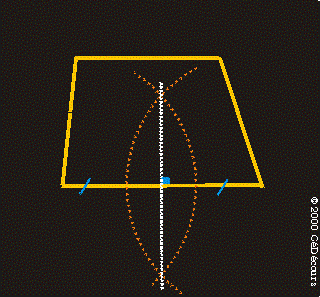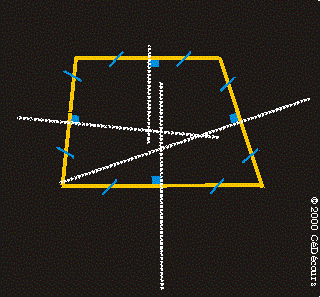
Pour un trapèze quelconque, les médiatrices ne sont pas forcément concourantes.

A ton avis, est-ce qu'il est possible de construire un cercle circonscrit pour ce trapèze quelconque ?