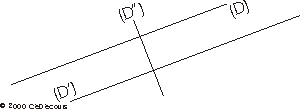
droites confondues, propriétés des angles
droites perpendiculaires
Deux droites parallèles ont le même coefficient directeur, c'est à dire la même pente.
On dit que deux droites parallèles ont la même direction.
Deux droites parallèles qui ont un point commun sont nécessairement confondues.
Des droites parallèles distinctes n'ont aucun point commun.
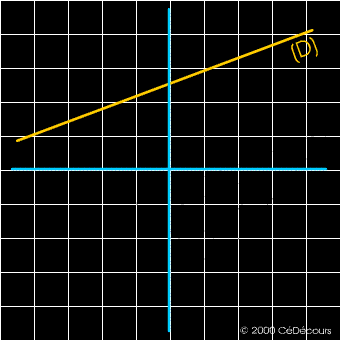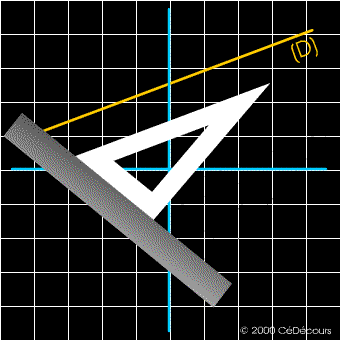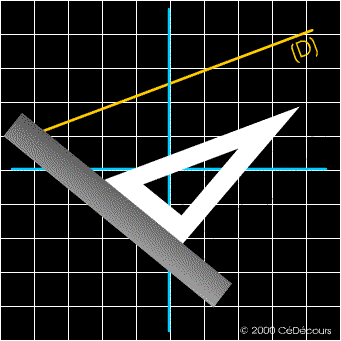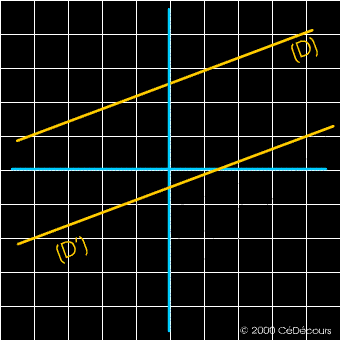
Exemple :
La construction de droites parallèles s'effectue avec une équerre et une règle.
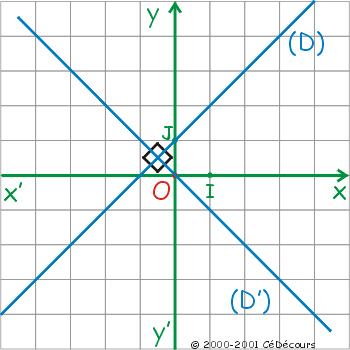
Les droites (D) et (D') sont parallèles et distinctes.
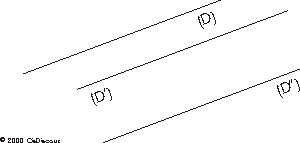
Si deux droites sont parallèles entre elles et que l'une d'entre elle est parallèle à une 3ème droite, alors l'autre aussi.
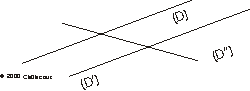
Deux droites distinctes du plan non parallèles sont sécantes et leur point d'intersection est toujours unique.
Si deux droites sont parallèles entre elles et que l'une d'entre elles est sécante à une 3ème droite, alors l'autre aussi.
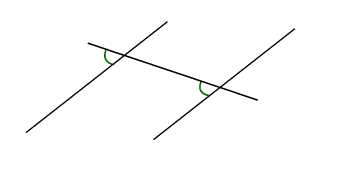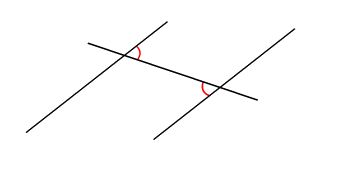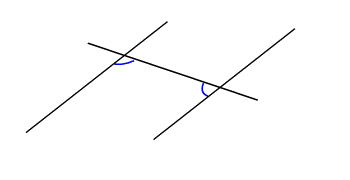
Propriétés des angles de deux droites parallèles :
- Les angles correspondants sont égaux (angles verts)
- Les angles situés de part et d'autre de la sécante entre les deux droites parallèles (et non adjacents) sont égaux (angles rouges)
- Les angles intérieurs qui sont situés du même côté de la sécante sont supplémentaires (angles bleus)
Deux droites perpendiculaires sont sécantes et se croisent avec un angle droit.
Par un point du plan, passent une infinité de droites de ce plan.
Toutes ces droites sont sécantes et ont un point d'intersection commun.
Si deux droites sont perpendiculaires à une même 3ème droite, alors ces deux droites ont la propriété d'être parallèles.