L'espace géométrique dans lequel nous vivons est un espace à 3 dimensions (3D) , la 4ème dimension est souvent interprétée comme celle de l'échelle du temps (4D) et la 5ème dimension n'est pas pour l'instant une réalité tangible sauf au cinéma !
Avec le plan, nous allons étudier un espace à 2 dimensions (2D) :
on y repèrera des objets géométriques élementaires, comme les points, les droites et les segments, par leurs coordonnées ou leurs équations exprimées en utilisant un repère orthonormé.
Cet écran, ou encore ta feuille de cahier matérialisent une portion de plan, plaçons-y un point origine, un axe orienté horizontal, appelé axe des abscisses et un axe orienté vertical, appelé axe des ordonnées, perpendiculaires entre eux et définissons les unités de longueurs pour chaque axe (échelle en abcisse et en ordonnée) : voila un premier repère orthogonal défini !
Si la même unité de longueur est utilisée pour l'axe des abscisses et l'axe des ordonnées, c'est un repère orthonormé !
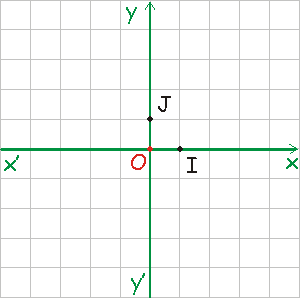
Le repère orthonormé (O, I, J) est défini par :
* son point d'origine dénommé par la lettre O,
* des points appelés I et J positionnés à la première graduation unité en abscisse et en ordonnée définissent l'unité de longueur. I et J sont aussi appelés les points unitaires.
On utilise aussi parfois une notation avec des vecteurs que tu verras dans le parcours n° 4 de ce tome 1 de MATHS SOLUTIONS.
Un repère orthonormé peut aussi être défini par son origine O et l'axe des abscisses qui s'appelle "x'x" et celui des ordonnées qui s'appelle "y'y " .
Attention : chacune de ces lettres ou des valeurs d'échelle peuvent changer : alors, sois vigilant en lisant les énoncés d'exercice, utilise bien les notations qui sont demandées. "x" et "y" sont souvent utilisés mais pas toujours !
Un point est un être géométrique sans dimension, il est désigné par une lettre majuscule : point A, par exemple.
Tout point d' un plan muni d'un repère orthonormé (O, I , J) est repéré à l'aide de ses coordonnées : l'abscisse et l'ordonnée.
Souvent appelées xA et yA pour un point A, elles sont notées entre parenthèses séparées d'un point virgule :
A ( xA ; yA )
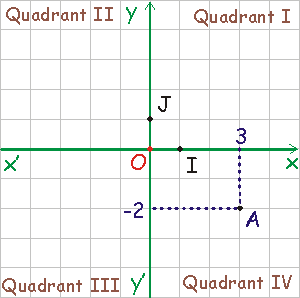
Exemples :
Coordonnées du point origine :
O ( 0 ; 0 )
Coordonnées des points unitaires I et J :
I ( 1 ; 0 )
J ( 0 ; 1 )
et coordonnées du point A :
A ( 3 ; - 2 )
Tu remarqueras que l'abscisse de A est positive mais son ordonnée est négative.
A est situé dans le IVème quadrant.
Les points du Ier (1er) quadrant ont des coordonnées :
* abscisse positive, ordonnée positive
Les points du IIème (2ème) quadrant ont des coordonnées :
* abscisse négative, ordonnée positive.
Les points du IIIème (3ème) quadrant ont des coordonnées :
* abscisse négative, ordonnée négative
Les points du IVème (4ème) quadrant ont des coordonnées :
* abscisse positive, ordonnée négative.
Soit le repère orthonormé (O, I, J) . On utilise l' échelle 1 unité : 3 cm.
Pour placer le point M de coordonnées : M(0,5 ; -2)
Effectuons la conversion d'échelle :
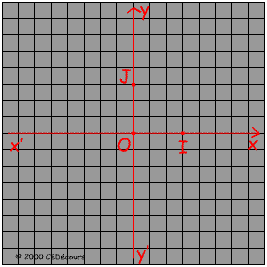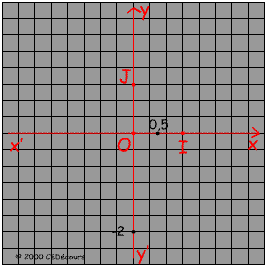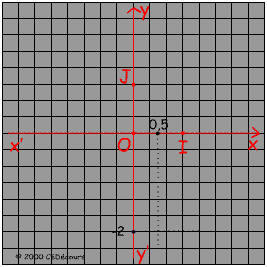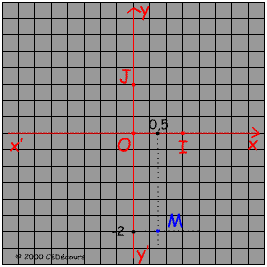
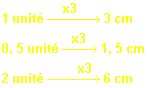
Positionnons l'abscisse x = 0,5 à 1,5 cm de l'origine et et l'ordonnée y = -2 à 6 cm de l'origine sur les axes x'x et y'y respectivement.
Le point M est situé à l'intersection des droites perpendiculaires aux axes menées de ces positions.