Cercle circonscrit. Cercle tangent.
-1ère définition : Le cercle de centre O et de rayon R est une ligne courbe fermée dont tous les points M sont situés à une égale distance R du point O.
-2ème définition : Par les 3 points non alignés et distincts A, B et C, il ne passe qu'un seul cercle et un seul. Un cercle peut donc aussi être défini de façon unique par la donnée de 3 points distincts non alignés.
Un arc de cercle est une portion du cercle limitée par les deux points distincts A et M du cercle :
Les points A et M délimitent aussi un segment [AM] : c'est la corde qui sous-tend l'arc de cercle.
Une corde est un segment qui joint deux points distincts d'un cercle.
Une corde qui passe par le centre est un diamètre du cercle.
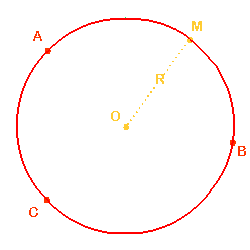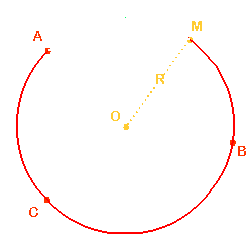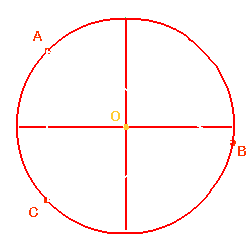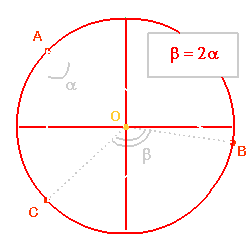
L'angle au centre est égal au double de l'angle inscrit :
Ce cercle est circonscrit au triangle ABC : c'est le cercle qui passe par les trois sommets de ce triangle. Le centre de ce cercle peut s'obtenir par construction : c'est le point de concours des 3 médiatrices des côtés. (Cette construction est expliquée au parcours n°1 de ce tome 1 de MATHS SOLUTIONS).
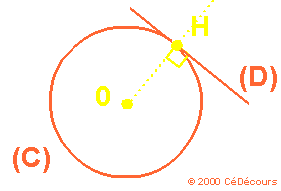
Lorsqu'une droite (D) et un cercle (C) sont tangents, il existe un seul point H commun au cercle et à la droite.
De plus, la droite (OH) est perpendiculaire à la droite (D) :