Dans certaines situations, il va falloir combiner les relations apportées par le théorème de Pythagore, les rapports trigonométriques et tes connaissances géométriques de base pour trouver les longueurs ou les angles inconnus d'un triangle rectangle.

Exemple : Soit un losange ABCD de côté 3,2 cm et dont l'angle de sommet C a pour mesure 61°. Les deux diagonales sont sécantes en leur milieu O.
Nous allons résoudre le triangle A0D

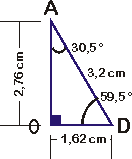
D'abord, reportons ces informations sur un schéma à l'échelle (cela nous permettra ensuite d'effectuer une vérification rapide de nos résultats) :

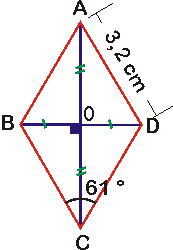
Ensuite, mettons en évidence les longueurs et les angles connus et inconnus du triangle :

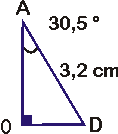
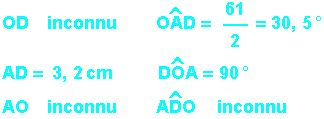
La présence de l'angle droit permet d'établir une première relation grâce au théorème de Pythagore :

La présence de l'angle droit permet d'établir une deuxième, troisième et quatrième relations grâce aux rapports trigonométriques :

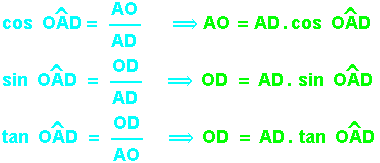
La propriété de la somme des angles dans un triangle permet d'établir une cinquième relation :

Nous avons l'embarras du choix pour résoudre le triangle !
Bien sûr, ce qui nous intéresse est de trouver les résultats le plus vite possible avec le moins de calculs intermédiaires possibles :
Compte tenu des données, la méthode la plus directe est de déterminer les deux longueurs inconnues grâce aux 2 premières relations trigonométriques :

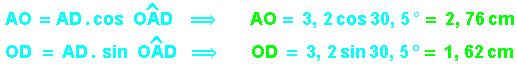
Puis, le 3 ème angle en utilisant la somme des angles :

Enfin vérifions nos résultats en utilisant la relation de Pythagore, la 3ème relation trigonométrique ou le dessin à l'échelle :

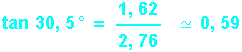
L'étape de la vérification est indispensable si tu veux progresser dans ce type d'exercices : personne n'est à l'abri d'une erreur de calcul, donc il est important d'avoir plusieurs méthodes pour recouper tes résultats et repérer les erreurs éventuelles...