Pour trouver des angles ou des longueurs inconnues dans un triangle quelconque, nous allons établir de nouvelles relations.
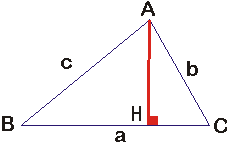
La hauteur [AH] menée de A fait apparaître deux triangles rectangles AHC et ABH. Nous pouvons utiliser des rapports trigonométriques pour évaluer de façon différente la longueur AH :
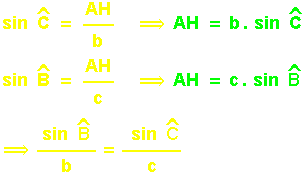
Ces relations sont très utiles dans le triangles quelconque et peuvent être établies pour les 3 angles, ce sont "les relations du sinus" :
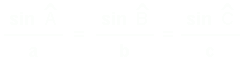
La figure ci-dessous a été tracée avec un logiciel de PAO qui permet de mesurer les cotes et les angles qui sont indiquées sur le schéma. Vérifie que les 3 rapports de la formule des sinus sont égaux à 0,099 (valeur approchée au millième près) :
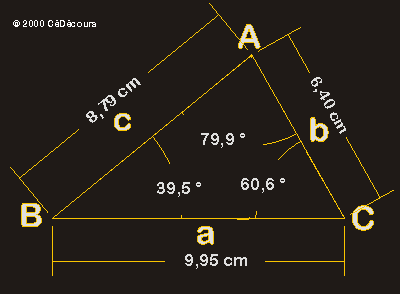
Le rapport des sinus ci-dessus est aussi égal à l'inverse du diamètre du cercle circonscrit au triangle : tu pourras le vérifier en construisant le cercle circonscrit à ce triangle.
Tu trouveras que le cercle circonscrit a un diamètre d'environ 10 cm !
On utilise aussi parfois un ensemble de 3 relations dites "du cosinus" pour le triangle quelconque. la première relation est :
a2 = b2 + c2 - 2bc cos Â.
Les deux autres relations sont obtenues en effectuant des permutations circulaires des noms des longueurs et des angles...