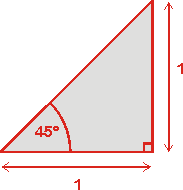
Une équerre rectangle isocèle contient deux angles à 45°. Supposons que les deux côtés ont une même longueur égale à l'unité, alors nous pouvons déterminer les rapports trigonométriques de cet angle en calculant grâce au théorème de Pythagore la longueur de l'hypoténuse :

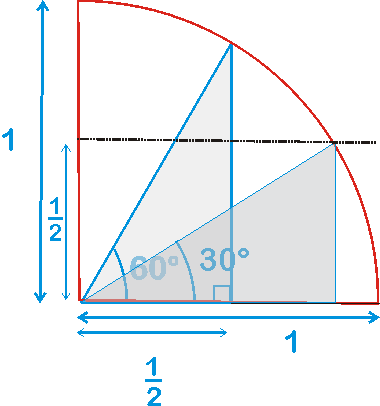
Pour retrouver les rapports trigonométriques des angles à 30° et 60°, on utilise des triangles inscrits dans le 1er quadrant du cercle trigonométrique, l'hypoténuse de ces triangles a une longueur égale à 1.

Pour chacun des deux triangles, deux longueurs sont directement lues sur la figure :
- pour l'angle à 30°, la longueur de l'hypoténuse est 1 et la longueur du côté opposé est égale à 1/2.
- pour l'angle à 60°, la longueur du côté adjacent est 1/2 et la longueur de l'hypoténuse est égale à 1 (rayon du cercle).
La 3ème longueur inconnue est déterminée en utilisant le théorème de Pythagore dans un triangle rectangle.

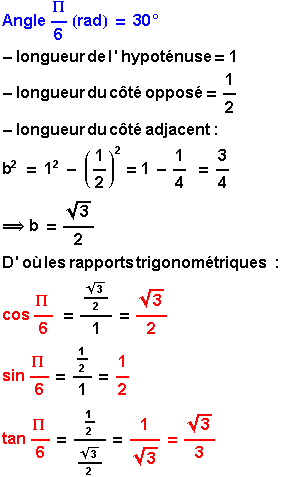
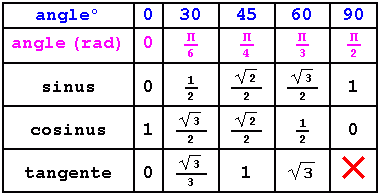
Voici le tableau des rapports trigonométriques pour les angles usuels. Pour mieux retenir ces valeurs, tu remarqueras que :
- les sinus et les cosinus de 30° et 60 ° sont croisés, leurs tangentes sont inverses l'une de l'autre. (c'est une propriété générale pour des angles complémentaires)
- le sinus de 45° est égal au cosinus, donc la tangente de 45° est égale à 1.
- attention à la tangente de 90° : elle n'existe pas (pour la trouver, il faudrait effectuer une division par 0, ce qui est n'est pas possible à ce niveau)