A partir d'un parallélogramme ABCD, nous traçons les bissectrices des angles de sommet A et C. Nous appelons A' et C' les points d'intersection de ces bissectrices avec les côtés opposés des angles correspondants :

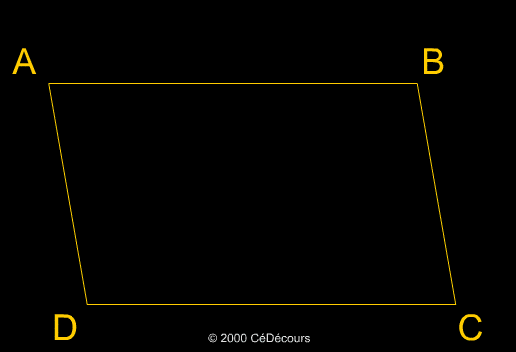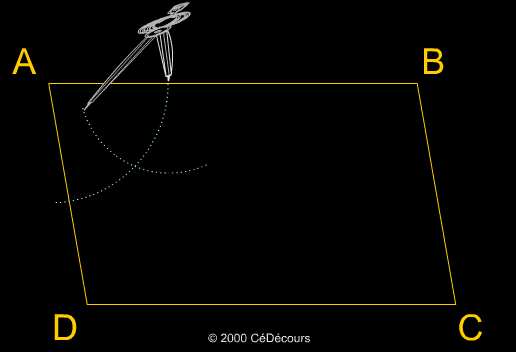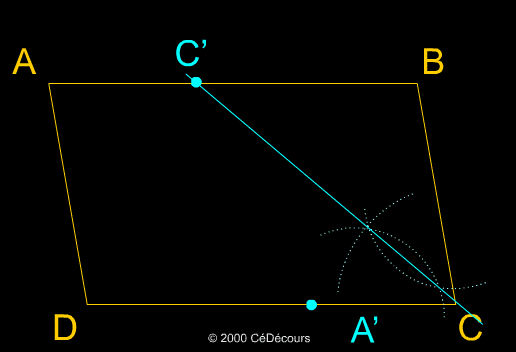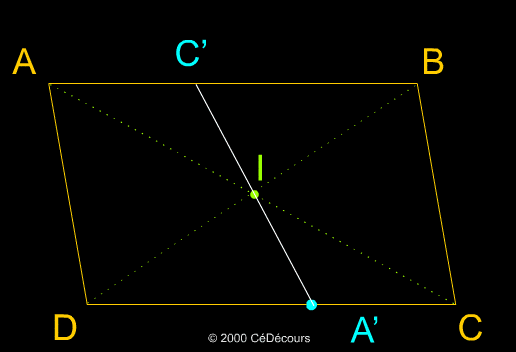
I est le centre de gravité du parallélogramme, c'est le point d'intersection des diagonales.

Comme tu peux le constater, les points A' , C' et I semblent bien alignés.

Raisonnons à l'aide de la symétrie centrale de centre I pour le prouver :

L'image de A est C et l'image de B est D par cette symétrie.
Par conséquent, l'image de la droite (AB) est la droite (CD) (l'image d'une droite par une symétire est une droite).
L'intersection de la bissectrice de l'angle de sommet A et de la droite (DC) a pour image l'intersection de la bissectrice de l'angle de sommet C et de la droite (AB) .
Les deux points A' et C' sont donc images l'un de l'autre par cette symétrie centrale :
La conséquence est immédiate, ils sont alignés sur la même droite et leur distance au centre I est égale !

Ce raisonnement logique constitue la démonstration (la preuve) de la propriété visualisée ci-dessus.