L'image d'un point M par une symétrie centrale de centre 0 est le point M' tel que O soit le milieu du segment [MM']. La construction s'effectue avec un compas et une règle.

La symétrie centrale est une transformation géométrique qui a de nombreuses propriétés, elle conserve :
- les distances,
- les angles
- les milieux
Ces objets sont des invariants par symétrie centrale.
Observe bien l'animation : tu trouveras des distances, des angles et un milieu qui se conserve !
Par contre, que penses-tu de la lettre A, est-ce qu'elle est invariante par symétrie centrale ? Est-ce que la lettre A aurait été invariante par symétrie axiale (d'axe vertical) ?
Entraîne-toi à représenter les images par symétrie centrale les images des points avec un compas et une règle. N'oublie pas que :
- 2 points distincts définissent une droite de façon unique
- 3 points distincts non alignés définissent un cercle de façon unique.
Tu retrouveras les propriétés de cette transformation géométrique :
l'image d'une droite est une droite
l'image d'un cercle est un cercle de même rayon
l'image un carré ou un rectangle est de même nature et de même dimension.
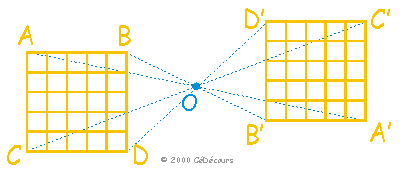
La symétrie centrale conserve aussi les aires et les propriétés de parallélisme et d'orthogonalité :
- 2 droites parallèles (perpendiculaires) ont des images qui sont des droites parallèles (perpendiculaires).
- 1 objet d'aire 25 m2 a une image qui a la même aire de 25 m2
Il n'est en aucun cas permis de télécharger ou d'enregistrer les images et animations présentées ci-dessus.