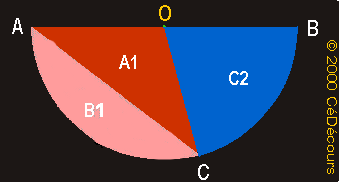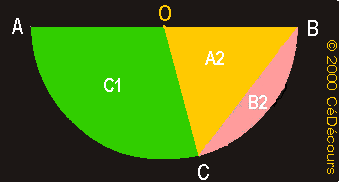
Volumes, surfaces et périmètres : fiche aide-mémoire n° 7
CALCULS D'AIRES
Les deux surfaces S1 et S2 ne sont pas usuelles. Elles sont délimités d'un côté par un arc de cercle, et de l'autre par un segment rectiligne. Pour calculer leurs aires B1 et B2, on ne pourra pas utiliser directement le formulaire...

Mais tu peux reconnaître dans cette figure, des triangles et des secteurs angulaires pour lesquels il sera possible de calculer l'aire à partir du formulaire.

Observe bien !
Tu obtiendras les aires B1 et B2 en effectuant la différence des aires du secteur angulaire et du triangle correspondant :
B1 = C1 - A1
 B2 = C2 - A2
On note C1 l'aire (en cm2) du secteur angulaire de rayon R = 2,5 cm et d'angle 106°.
C1 = 3,14.(2,5)2.106/360 = 5,78

On note A1 l'aire (en cm2) du triangle OCA avec AC = 2,5 cm et la hauteur OM = 1,5 cm :
A1 = 0,5.2,5.1,5 = 1,87

On obtient l'aire B1 (en cm2) :
B1 = C1 - A1 = 5,78 - 1,87 = 3,91

En suivant un raisonnement analogue, tu trouveras la valeur de l'aire B2 de la surface S2.
Vérifie ton résultat en effectuant l'addition de toutes les aires que tu as trouvées :

C1 + C2 = A1 + B1 + A2 + B2

" L'aire du demi-disque est égale à l'aire des deux triangles et des deux surfaces S1 et S2."
© 1999-2000 CéDécours