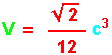| PYRAMIDE | SPHERE | CUBE |
| PARALLELEPIPEDE | PRISME DROIT | TETRAEDRE |
| TRONC DE CONE | ||
Cette pyramide à base carrée est engendrée par la rotation de son apothème [SM] : le point M décrit le pourtour du carré ABCD de côtés de longueur c.
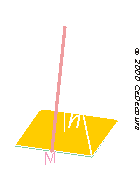
La formule du volume s'exprime à l'aide de l'aire A de la base carrée ABCD et de la hauteur h :
V = 1/3 . AIRE DE LA BASE . HAUTEUR
Avec
:
AIRE DE LA BASE = c²
HAUTEUR = h
Exemple :si c = 2 cm et h = 3cm
Vérifie que tu trouves V = 4 cm3

Exemple :
si R = 2 cm
Vérifie que tu trouves V =33,5 cm3

Exemple :
si c = 2 cm
Vérifie que tu trouves V = 8 cm3

Pour le parallélépipède dont les longueurs des arêtes sont respectivement a, b et c :
Exemple :
si a = 3 cm
b = 2 cm
c = 1,5 cm
Vérifie que tu trouves V = 9 cm3

Exemple :
si A = 5 cm2
h = 2 cm
Vérifie que tu trouves V = 10 cm3

Pour le tétraèdre régulier dont toutes les arêtes ont pour longueur c :
Exemple :
si c = 4cm
Vérifie que tu trouves V = 7,5 cm3
A partir de ces formules de calcul, tu peux calculer le volume d'un solide obtenu par transformation d'un solide usuel, comme, par exemple, le tronc de cône :

Il est possible de retrouver cette formule en partant des formules des cônes de rayon R et R' .
Soustraie les deux volumes, puis en utilisant le théorème de Thalès, trouve h'/h en fonction de R'/R .
Un peu de calcul algébrique sera nécessaire !
Exemple :
si R = 2 cm
R' = 1,5 cm
h = 2 cm