Illustration géométrique des identités remarquables

 

Observe bien l'animation ci-dessous :
On forme un grand carré de côté a , il a pour aire a2.
Ensuite, on retire une tranche rectangulaire de largeur b et de longueur a de chaque côté.
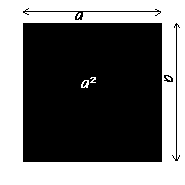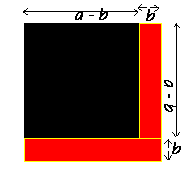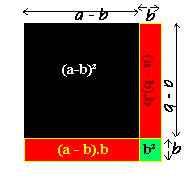
Cela permet de former deux rectangles (rouge) d'aire a . (b - a) et un carré (vert) d'aire b2.

Tu peux visualiser toutes les aires qui interviennent dans la formule de l'identité remarquable :

- remarque d'abord que :
  (a - b) . (a - b) = (a - b)2
- puis effectue la somme de toutes les aires :
  a2 = (a - b)2 + 2b(a - b ) + b2
- en développant le produit : 2b(a - b) = 2ba - 2b2
  a2 = (a - b)2 + 2ab - b2
- ce qui donne bien l'égalité :
  (a - b)2 = a2 - 2ab + b2
Exemples d'utilisation des identités remarquables en calcul algébrique :
Expressions à développer :
Expressions à factoriser :
Solutions :
Copyright © 2000 CéDécoursTM - Tous droits de propriété intellectuelle et industrielle réservés
Il n'est en aucun cas permis de télécharger ou d'enregistrer les images et animations présentées ci-dessus.