formules
Les trois identités remarquables sont des développements ou factorisations d'expressions particulières :
1 - Développement du carré d'une somme :
(a + b)2 = a2 + 2ab + b2
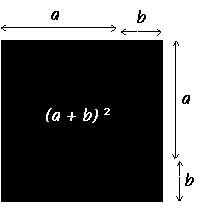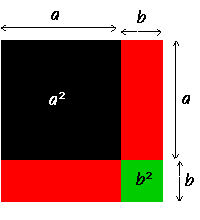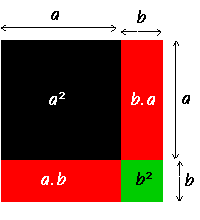
2 - Développement du carré d'une différence :
(a - b)2 = a2 - 2ab + b2
3 - Factorisation de la différence de deux carrés :
a2 - b2 = (a + b) . (a - b)
L'animation présente une illustration géométrique pour l'identité remarquable sur le carré d'une somme.
Les identités remarquables peuvent être utilisées pour effectuer plus facilement certains calculs numériques sans calculatrice :
- Le produit de deux nombres symétriques :
64 . 56 = (60 + 4) . (60 - 4) = 602 - 42 = 3600 - 16
Finalement, 64 . 56 = 3584
- Le carré d'un nombre terminé par 1 ou 9 :
512 = (50 + 1)2 = 502 + 2 . 50 + 1 = 2500 + 100 + 1
On obtient : 512 = 2601
492 = (50 - 1)2 = 502 - 2 . 50 + 1 = 2500 - 100 + 1
On obtient : 492 = 2401
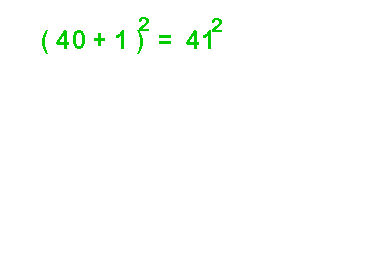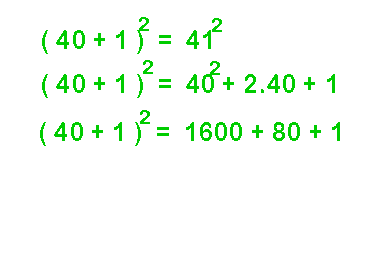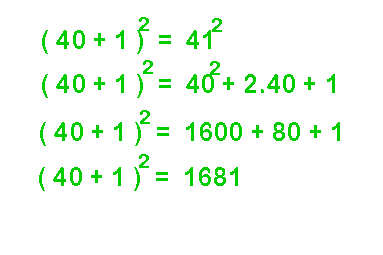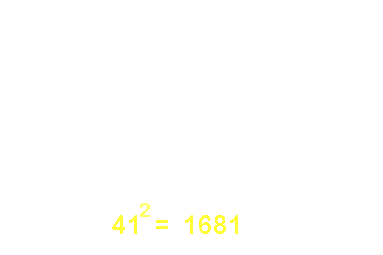
Calcule rapidement et sans calculatrice le produit de 76 par 74 ainsi que le carré de 61 et 59
Pour résoudre l'équation du 2ème degré suivante : 16 x 2 - 9 = 0, tu peux utiliser une identité remarquable qui te permettra de transformer cette équation du second degré en un produit de deux équations du 1er degré.
Quelle est l'identité remarquable utilisée ?

Il n'est en aucun cas permis de télécharger ou d'enregistrer les images et animations présentées ci-dessus.