Grâce à la 3ème identité remarquable, tu peux résoudre une équation du second degré de la forme x2 - a2 = 0 , en te ramenant à une équation formée du produit de 2 équations du 1er degré :
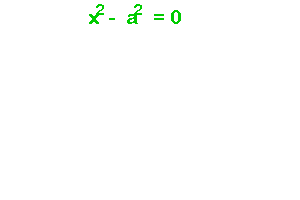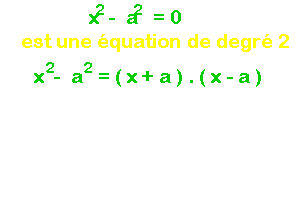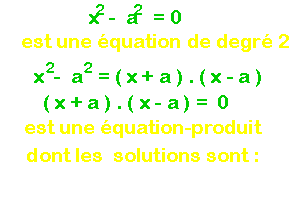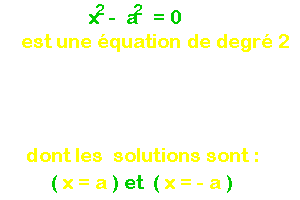
Pour qu'un produit de facteurs soit nul, il faut et il suffit que l'un des facteurs soit nul. L'équation se décompose alors en deux autres :
Lorsque l'on factorise une expression algébrique du second degré en produit de deux expressions du 1er degré, cela peut permettre de résoudre une équation du second degré en se ramenant à la résolution de deux équations du 1er degré :
Soit l'équation à résoudre :
10x2 - 6x = 0
On peut mettre en facteur "2x" : 10x2 = 2x . 5x et 6x = 2x . 3
L'équation se ramène à une équation-produit :
L'équation admet donc deux solutions :
Il n'est en aucun cas permis de télécharger ou d'enregistrer les images et animations présentées ci-dessus.