La section plane d'un solide est la figure géométrique obtenue lorsque l'on coupe ce solide par un plan. Etudions ces figures pour le cube, le parallélépipède, le cylindre, le cône et la pyramide.
Un cube ABCDEFGH est un solide délimité par 6 faces carrées de côté a identiques.
Coupons ce cube par un plan parallèle à l'une des faces :
La section plane ainsi obtenue est une surface de même nature que les faces : c'est un carré de côté a.
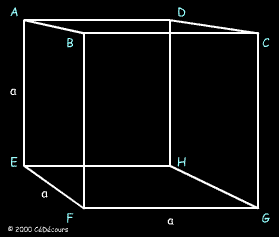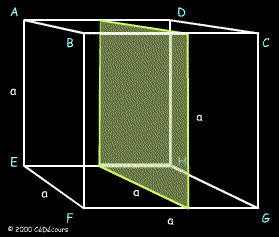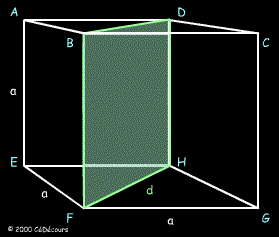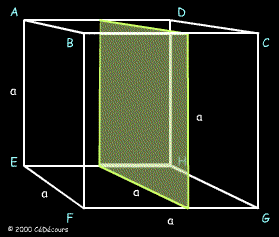
Coupons ce cube par le plan qui contient les diagonales des bases : la section est le rectangle BFHD de largeur a et de longueur d à déterminer.
Formons la relation de Pythagore pour la longueur inconnue d = BD = FH :
d2 = a2 + a2 = 2 a2
Pour trouver d, il faut prendre la racine du produit 2a2, qui est égale au produit des racines :

Un parallélépipède (pavé) rectangle est un solide délimité par 6 faces rectangulaires.
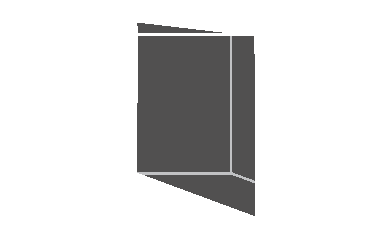
Coupons ce pavé par un plan parallèle à l'une de ses faces. Les sections obtenues sont des rectangles.
Les longueurs et les largeurs des rectangles se "lisent" sur le schéma.
Ci-contre, le rectangle a pour largeur et longueur les longueurs des arêtes correspondantes :
a et b.
Un cylindre de révolution possède un axe, une hauteur h et des disques de bases identiques de rayon R .
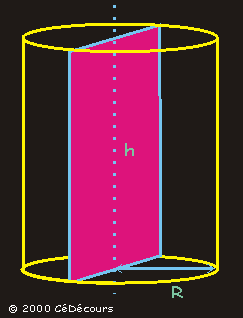
Si on coupe un cylindre par un plan parallèle à sa base, la section obtenue est un cercle de rayon R.
Coupons ce cylindre par un plan qui contient son axe de révolution. La section obtenue est un rectangle qui a pour longueur et largeur :
2R et h.
Un cône de révolution possède un axe, une hauteur h et un disque de base de rayon R
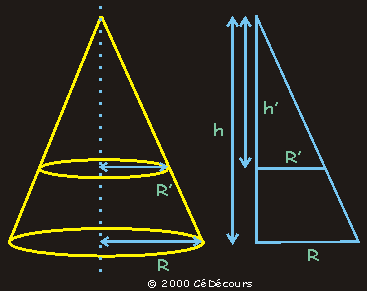
Coupons ce cône par un plan parallèle à sa base à une distance h' de son sommet. La section obtenue est un cercle de rayon R' dont la valeur s'obtient en appliquant le théorème de Thalès :
les rapports R'/R et h'/h sont égaux.
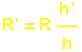
Une pyramide de hauteur h à base carrée possède 4 faces triangulaires.
Si on coupe cette pyramide par un plan parallèle à sa base et à une distance h' de son sommet.
La section obtenue est un polygone de même nature que sa base, ici c'est un carré de côté a' dont la valeur est obtenue comme pour le cône grâce au théorème de Thalès :
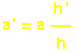
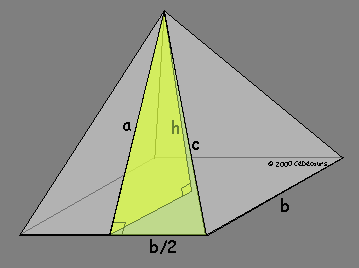
Coupons cette pyramide par le plan de symétrie parallèle à l'un des côtés de sa base qui passe par le sommet. La section plane obtenue est un triangle isocèle. Les deux côtés semblables ont la longueur de l'apothème que l'on note maintenant avec la lettre a.
Calculons l'apothème en fonction de la hauteur h de la pyramide et de b la longueur d'un côté de la base carrée en appliquant le théorème de Pythagore :
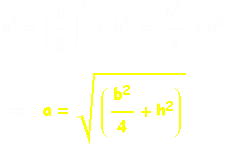
Il n'est en aucun cas permis de télécharger ou d'enregistrer les images et animations présentées ci-dessus