| SOMME | PRODUIT |
| DIFFERENCE | DIVISION |
| DISTRIBUTIVITE, PRIORITE & PARENTHESE | |
Lorsque l'on effectue des additions où des lettres apparaissent, on parle de somme algébrique. Quand les sommes ne comprennent que des nombres, ce sont des sommes arithmétiques ou numériques.
En calcul algébrique, on mélange des lettres et des nombres. Dans une somme algébrique, on donne le nom de termes aux lettres séparées par des signes +.
La somme de plusieurs termes est indépendante de l'ordre de ses termes :
Si un ou plusieurs termes sont remplacés par leur somme déjà effectuée (repérée à l'aide de parenthèses) à l'intérieur de l'expression algébrique, cela ne change pas la valeur de l'expression algébrique :
La somme d'un nombre a quelconque et du nombre 0 est toujours égal à :
On dit que le nombre 0 est neutre pour l'addition.
La somme de 2 termes a identiques est égale au double de a :
La somme de 3 termes a identiques est égal au triple de a :
La somme de 4 termes a identiques est égal au quadruple de a :
On peut définir la différence de deux termes à partir de la connaissance de la somme de deux termes :
La différence de a et b est égal à un nombre c tel que la somme de c et de b est égale à a :
Soustraire à un nombre b à un nombre a peut s'effectuer aussi naturellement à partir de la connaissance du nombre opposé à b, qui est égal à - b :
a - b = a + (- b )
Attention, lorsqu'il y a un regroupement d'opérations déjà effectuées entre parenthèses précédé d'un signe - , il ne sera possible d'enlever la parenthèse qu'à la condition de changer le signe de tous les termes qui y sont compris :
a - (b - c) = a - b - (- c ) = a - b + c
L'opposé du nombre a est égal au nombre - a.
Et l'opposé du nombre - a est égal au nombre - (- a) = + a = a
Notations des produits : en calcul algébrique, il est possible de noter la multiplication avec une croix, un point, ou... rien du tout.
Tu as sans doute remarqué que les différentes écritures coexistent :
Tu peux utiliser l'une ou l'autre selon que tu veux faire apparaître l'opération ou non.
Termes d'un produit : chaque terme d'un produit est appelé "facteur" :
L'expression algébrique a . b est le produit de deux facteurs : l'un est "a", l'autre est "b"
Le produit de plusieurs facteurs est indépendant de l'ordre de ses facteurs :
a . b = b . a
a . b . c = a . c . b = b . a . c = b . c . a = c . a . b = c . b . a
Si un ou plusieurs facteurs sont remplacés par leur produit déjà effectué (repéré à l'aide de parenthèses) à l'intérieur de l'expression algébrique, on obtient un produit contenant tous les facteurs cela ne change pas la valeur de l'expression algébrique :
Le produit d'un nombre a quelconque par le nombre 1 est toujours égal à a :
On dit que le nombre 1 est neutre pour la multiplication.
Le produit d'un nombre a quelconque par le nombre -1 est égal à l'opposé de a :
a . ( - 1 ) = - a
Si dans un produit de plusieurs facteurs, l'un est nul, alors le produit est nul :
a . b . c . 0 . d . e = 0
Le signe d'un produit de plusieurs facteurs est :
* positif si le nombre de facteurs négatifs est pair ou nul
* négatif si le nombre de facteurs négatifs est impair
Le produit de 2 facteurs a identiques est égal au carré de a :
a . a = a2
Le produit de 3 facteurs a identiques est égal au cube de a :
a . a . a = a3
Le produit de 4 facteurs a identiques est égal à :
a . a . a . a = a4
4 est appelé l'exposant de la puissance
En divisant le nombre a par le nombre b non nul, on forme le quotient de a par b qui est une fraction algébrique, couramment appelée rapport des deux termes a et b. Le rapport de a sur b est égal au nombre x tel que :
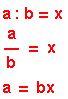
La division d'un nombre a quelconque par le nombre 1 est toujours égal à a :
On dit que le nombre 1 est neutre pour la division.
Le quotient de a par b non nul peut s'écrire comme le produit de a par l'inverse de b :
Toutes les divisions peuvent ainsi être remplacées par des multiplications, ce qui permet de simplifier les expressions qui contiennent des divisions successives comme (b et c non nuls) :
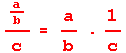
Cela permet aussi d'appliquer des propriétés des produits pour étudier les propriétés d'un rapport : par exemple, le signe d'un rapport a/b est égal au signe du produit de a par l'inverse de b, donc du produit ab.
Le produit de deux fractions algébriques s'effectue selon les mêmes règles que les produits de fractions numériques. On peut terminer le calcul précédent :
La division par le nombre 0 est impossible : on ne l'écrira donc pas !
La multiplication est distributive par rapport à l'addition et la soustraction : lorsque l'on forme le produit d'un facteur avec une somme généralisée (sommes et différences), il faut multiplier le facteur par chacun des termes de la somme.
on obtient finalement en réécrivant chaque produit le résultat bien présenté :
La division aussi est distributive par rapport à l'addition et la soustraction : lorsque l'on forme le rapport d'une somme généralisée (sommes et différences) et d'un facteur x non nul, il faut diviser chacun des termes de la somme par le facteur x.
En réécrivant chaque rapport, on obtient le résultat bien présenté :
Dans une expression algébrique complexe qui comprend plusieurs opérations successives, on doit appliquer des règles de priorité : la multiplication et la division sont prioritaires par rapport à l'addition et la soustraction.
x + y . a + b = x + ay + b
Par contre, lorsqu'il y a des parenthèses pour indiquer les opérations à effectuer, elles sont prioritaires et il faut bien les respecter.
(x + y) . (a + b) = (x + y) . a + (x + y). b = ax + ay + bx + by
Tu as dû observer sur ces deux exemples qui comprennent les mêmes lettres et opérations dans le même ordre, que le résultat est bien différent lorsque les règles de priorité s'appliquent automatiquement ou lorsqu'il y a des parenthèses qui indiquent les opérations déjà effectuées !
Il n'est en aucun cas permis de télécharger ou d'enregistrer les images et animations présentées ci-dessus