Dans une expression algébrique, nombres et lettres coexistent, les nombres ont une valeur fixe alors que lettres peuvent varier et changer de valeur....
On donne le nom de "variables" aux lettres puisque celles-ci peuvent prendre différentes valeurs.
Prenons une expression algébrique A qui contient deux variables x et a.
La forme littérale (avec des lettres) de A est donnée par :
A = ( 5 + a ) . x
La valeur numérique (avec des nombres) de l'expression A est obtenue en remplaçant dans celle-ci les variables par leur valeur numérique et en effectuant toutes les opérations.
La valeur numérique de A lorsque a = - 2 et x = 3 est égale à :
La valeur numérique de A lorsque a = 1/2 et x = - 4 est égale à :
![]()
Comme tu peux le constater la valeur numérique de l'expression algébrique A varie en fonction des valeurs des variables x et a.
Sais-tu effectuer toutes sortes d'opérations en calcul littéral et transformer les formules algébriques ?
Comment établir une expression algébrique à partir d'un énoncé ?
Dans l'énoncé, repérer les lettres qui interviendront dans l'expression algébrique et former les opérations les unes après les autres en respectant les imbrications.
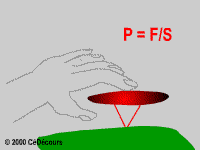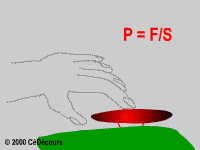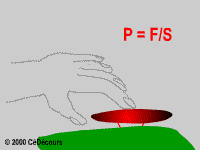
Prenons un énoncé simple d'une propriété du cours de physique :
La pression P est égale au rapport de la force F et de la surface S
![]()
Prenons un énoncé d'une propriété du cours de mathématiques :
Le produit de la somme de deux nombres par leur différence est égal à la différence des carrés de ces deux nombres.
Comme l'énoncé mentionne deux nombres, nous allons les désigner par deux lettres quelconques pour les matérialiser : soient x et y ces deux nombres.
Ensuite, décomposons l'énoncé :
"la somme de deux nombres" correspond à l'expression algébrique :
"la différence de deux nombres" correspond à l'expression algébrique :
Ecrivons le produit de la somme de deux nombres par la différence de deux nombres :
cela donne l'expression algébrique :
"la différence des carrés des deux nombres" correspond à l'expression algébrique :
x2 - y2
Terminons par l'égalité :
(x + y) . (x - y) = x2 - y2
Cette égalité est bien connue :
tu la rencontreras dans le cours sur les identités remarquables !
Pour établir ces formules à partir d'énoncés ou de schémas, tu devras savoir simplifier et transformer ces expressions algébriques. Entraîne-toi grâce aux conseils...

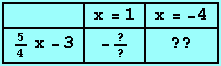
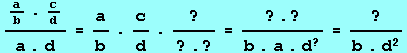
Il n'est en aucun cas permis de télécharger ou d'enregistrer les images et animations présentées ci-dessus.