| SIMPLIFICATION | TRANSFORMATION |
| PROPRIETES EGALITES | PROPRIETES INEGALITE |
| EXPRESSION A PARTIR D'UN SCHEMA | |
Pour simplifier une expression algébrique, on repérera d'abord toutes les opérations qu'il est possible d'effectuer entre les nombres présents et on observera attentivement si une ou plusieurs lettres se répètent :
On peut simplifier des sommes ou des différences algébriques lorsqu'une même lettre apparaît à plusieurs reprises :
a - ( b + 2a ) = a - b - 2a = - a + b
La simplification d 'un produit est possible dès que des facteurs semblables apparaissent dans un produit . Cela fait apparaître des carrés, des cubes ou des puissances plus élevées de ce facteur :
2 . a . 2 . a = 4a2
Il est possible de simplifier un rapport dans le cas où les deux termes ne comprennent que des multiplications et font apparaître des lettres semblables :
S'il y a des fractions qui apparaissent, les règles de calcul arithmétique pour les fractions s'appliquent, donc, par exemple, pour additionner ou soustraire des fractions algébriques, on doit réécrire les fractions avec un dénominateur commun :
Lorsque toutes les opérations sont présentes et que les expressions deviennent complexes, toutes les règles du calcul numérique et du calcul algébrique s'appliquent !
Exemple de simplification d'une expression complexe :
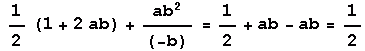
Il est indispensable de bien connaître les égalités élémentaires de transformation pour un simple rapport : (b et x non nuls)
Pour l'égalité de deux rapports, on forme le produit en croix pour mémoriser plus facilement la transformation : (a b x et y non nuls)
Lorsque deux rapports sont égaux, on observe de nouvelles propriétés remarquables sur les rapports formés à partir de la somme ou de la différence des numérateurs ou dénominateurs :
De plus, pour toutes les manipulations comprenant des rapports, il ne faut pas oublier que les règles de calcul sur les fractions s'appliquent : simplification, réduction au même dénominateur etc...
Si deux nombres a et b sont égaux, alors : a = b
le nombre placé à gauche de l'égalité est le 1er membre, et le nombre placé à droite est le 2nd membre.
On peut effectuer des opérations identiques pour chaque membre de l'égalité, quelque soit le nombre c, ce qui permet d'écrire de nouvelles égalités.
On peut ajouter ou soustraire un nombre c de chaque côté de l'égalité, celle-ci reste vérifiée :
a - c = b - c
On peut multiplier, diviser par un nombre c non nul de chaque côté de l'égalité, celle-ci reste vérifiée :
Si les nombres a b c et d non nuls sont égaux 2 à 2, alors, on forme deux égalités et on peut effectuer les quatre opérations (additionner, soustraire, multiplier et diviser) membre à membre :

Pour effectuer des additions et des soustractions sur des inégalités
Respectons les règles :
a
< b -----------› a + c <
b + c
a < b -------------› a - d <
b - d
"a
< b" + "c < d"
----------› a + c
< a +
d
Pour effectuer des multiplications sur des inégalités
Encore des règles :
a < b ----(si c > 0)------› a . c < b . c
a < b ----(si c < 0)------› a . c > b . c
"0 < a < b" . "0 < c < d" ----------› 0 < a . c < b . d
"a < b < 0" . "c < d < 0"----------› a . c > b . d > 0
Pour prendre l'inverse d'une inégalité
Toujours des règles :
a < b < 0 ----------› 1/b < 1/a < 0
Un terrain doit être traversé sur un côté par un chemin, sa surface est donc réduite. Quelle est la formule littérale qui donne l'aire du nouveau terrain en fonction des longueurs caractéristiques du problème ? Quelle est la différence d'aire entre l'ancien terrain et le nouveau terrain ? (On rappelle que l'aire d'un rectangle est égale au produit de sa longueur par sa largeur)
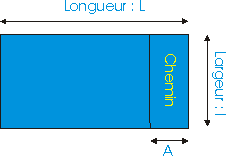
Longueur du nouveau terrain : L - A
Largeur du nouveau terrain : l
Aire du nouveau terrain : ( L - A ) . l
Aire de l'ancien terrain : L . l
La différence entre les deux :
- lue sur le schéma est égale à l'aire du rectangle constitué par le chemin : A . l
- calculée par différence :
L . l - (L - A) . l = Ll - L . I + Al = A . l
On obtient bien sûr la même formule littérale !
Il n'est en aucun cas permis de télécharger ou d'enregistrer les images et animations présentées ci-dessus