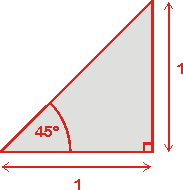
Une équerre rectangle isocèle contient deux angles à 45°. Supposons que les deux côtés ont une même longueur égale à l'unité, alors nous pouvons déterminer les rapports trigonométriques de cet angle en calculant grâce au théroème de Pythagore la longueur de l'hypoténuse :

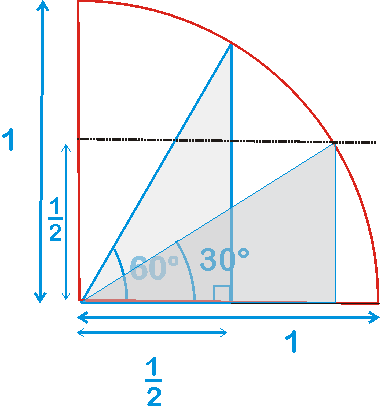
Pour retrouver les rapports trigonométriques des angles à 30° et 60°, on utilise des triangles inscrits dans le 1er quadrant du cercle trigonométrique, l'hypoténuse de ces triangles a une longueur égale à 1.

Pour chacun des deux triangles, deux longueurs sont directement lues sur la figure :
- pour l'angle à 30°, la longueur de l'hypoténuse est 1 et la longueur du côté opposé est égale à 1/2.
- pour l'angle à 60°, la longueur du côté adjacent est 1/2 et la longueur de l'hypoténuse est égale à 1 (rayon du cercle).
La 3ème longueur inconnue est déterminée en utilisant le théorème de Pythagore dans un triangle rectangle.

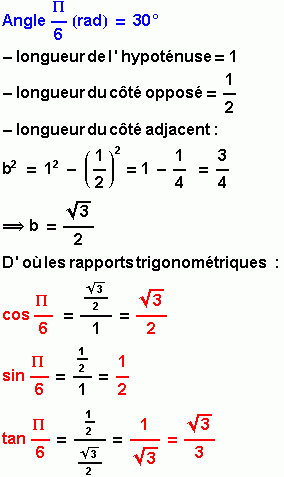
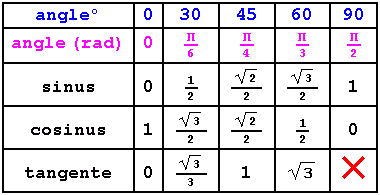
Voici le tableau des rapports trigonométriques pour les angles usuels. Pour mieux retenir ces valeurs, tu remarqueras que :
- les sinus et les cosinus de 30° et 60 ° sont croisés, leurs tangentes sont inverses l'une de l'autre. (c'est une propriété générale pour des angles complémentaires)
- le sinus de 45° est égal au cosinus, donc la tangente de 45° est égale à 1.
- attention à la tangente de 90° : elle n'existe pas (pour la trouver, il faudrait effectuer une division par 0, ce qui est n'est pas possible)

Angle de rapport trigonométrique donné

Lorsque l'on connait la valeur du sinus, du cosinus ou de la tangente d'un angle, il est possible de retrouver la valeur de cet angle : on utilise à ce niveau les fonctions Arc Sinus, Arc cosinus et Arc tangente de la calculatrice.
Ces fonctions sont accessibles différemment selon le modèle de calculatrice dont on dispose et ne donneront le résultat attendu que si tu sais aussi utiliser les différents modes d'unités d'angles de ta machine.

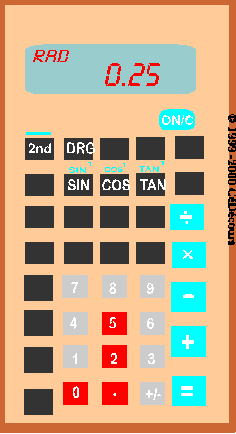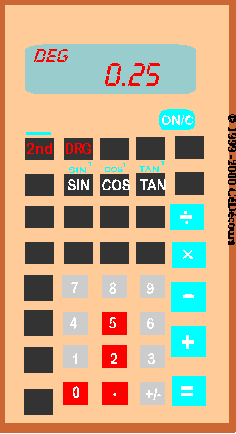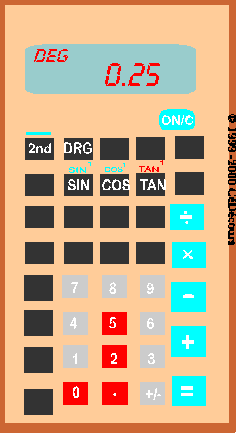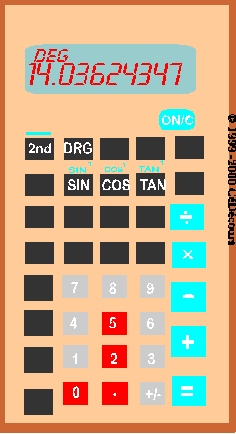
Pour obtenir un résultat en degré, ou en radian active le mode correspondant : en général DEG ou RAD (consulte la notice de ta calculatrice).
Par défaut certaines machines affichent les résultats en radian, d'autres en degré.

Exemple : On donne un rapport trigonométrique connu de l'angle  :
tan  = 0.25
Pour trouver la valeur de  en degrés, il faut s'assurer que la machine utilise les degrés comme unité d'angle. Si elle utilise les radians ou les grades, il faut changer : en général une touche DRG (DégréRadianGrade) permet d'effectuer la conversion.
Ensuite, on trouvera l'arc tangente en activant la touche TAN-1 (ou aussi INV TAN ou ATAN selon les modèles de calculatrices).
On trouve :
 = 14,04 ° (au centième près)
Vérifie toi-même que tu as trouvé le bon angle  :
tan(14,04°) = 0.25